经过近30年的发展，变分方法已经成为图像处理与分析的重要数学基础(Scherzer，2015；Paragios等，2006；Aubert和Kornprobst，2006；Chan和Shen，2005)，其中，图像恢复的变分模型具有基础地位。该类模型一般包含数据项和规则项，出于对图像特征保持的考虑，其规则项往往是非线性、非光滑，甚至是非凸的。这些特点不仅导致数值算法设计的困难，且其数值方法的计算效率往往较低，成为变分图像处理与分析模型工程应用的主要瓶颈之一(Kimmel和Tai，2019；Glowinski等，2016)。

以总变差(total variation，TV)(Rudin等，1992)为代表的一阶变分模型可以保持图像的边缘特征，是变分图像处理与分析问题的基础模型。为了克服基于原变量的时间步进方法(Rudin等，1992)和固定点迭代方法(Vogel和Oman，1996)计算效率低的问题，Chan等人(1999)提出了原—对偶变量方法(primal-dual method，PD)，Chambolle(2004)提出了经典的对偶方法(dual method，DM)，Goldstein和Osher(2009)提出了SB(split bregman) 方法。Wu和Tai(2010)证明，SB算法与增广Lagrange方法(augmented Lagrangian method，ALM)或交替方向乘子法(alternating direction methods of multipliers，ADMM)(Glowinski和Le Tallec，1989)是等价的。Daubechies等人(2004)以交替迭代优化为框架提出了经典的软阈值迭代算法(iterative shirinkage-thresholding algorithm，ISTA)。上述方法均为基于一阶导数或梯度的一阶方法，其收敛率为O (1/$k$)，$k$为迭代次数。

早在20世纪80年代初，Nesterov(1983)针对光滑凸目标函数的优化问题，基于函数外插或惯性加速的思想，通过设计适当的惯性参数，将基于梯度的方法的算法收敛率提高至O (1/$k^2$)，为变分图像处理模型的加速算法设计奠定了基础。Beck和Teboulle(2009a, b)针对组合目标函数结合Nesterov方法与ISTA方法提出了快速ISTA方法，即快速软阈值迭代算法(fast iterative shirinkage-thresholding algorithm，FISTA)。基于相似的思路，Beck和Teboulle(2014)提出了快速对偶方法(fast dual，FD)、Chambolle和Pock(2011)提出了快速原—对偶变量方法(fast PD，FPD)、Zhu和Chan(2008)提出了原—对偶变量混合梯度方法(primal-dual hybrid gradient，PDHG)，Goldstein等人(2014)提出了快速ADMM方法。该类加速方法设计的关键是最优惯性参数的设计，该参数依赖于目标函数的光滑度与凸性，但通常的变分图像处理模型往往局部强凸或完全非凸，导致这些参数估计困难或过分耗时，其惯性加速类算法会引起涟漪或振荡现象(O’Donoghue和Candès，2015)，达不到预期加速效果。改进的单调算法(Beck和Teboulle，2009b)、回溯算法(Goldstein等，2014)或重启动算法(O’Donoghue和Candès，2015)的研究成为近年惯性加速方法实用化的重要方向之一。单调类算法依据相邻两次迭代结果构造惯性加速，回溯方法是通过向后寻找能够使得能量值下降的最小步长来保证算法能量值下降，重启动算法则在能量非下降时重置初始参数，这些方案均能避免振荡现象，并保持算法收敛率仍为O(1/$k^2$)，该研究正在成为凸优化计算领域的热点问题之一(Kim和Fessler，2018；Calatroni和Chambolle，2019；Buccini等，2020)。但相关研究和应用在计算机视觉领域还限于基于一阶导数的变分图像处理模型及经典的Lasso模型(陈少利，2017；李启朋，2018；李星等，2019；潘树林等，2019)。

基于二阶导数的变分模型可有效克服一阶导数模型引起的阶梯效应问题，其规则项的形式多样，且由于模型的非线性、非光滑性和非凸性，其计算效率低的问题更加突出。Bredies等人(2010)直接将Nesterov型加速方案应用于基于二阶导数的总广义变差(total generalized variation，TGV)模型计算；Liu等人(2012)设计了基于总海森(total Hessian，TH)变分模型的快速PDHG算法；Yashtini和Kang(2016)则用相同的方法设计了基于欧拉弹性能(Euler’s elastica，EE)的算法设计。Bredies等人(2010)的方法包含2个凸的非光滑规则项，Liu等人(2012)的方法包含1个凸的非光滑规则项，Yashtini和Kang(2016)的方法包含非凸、非光滑规则项，除快速算法本身可能引起的振荡问题，非凸性亦可引起能量上升，但前期研究均未考虑这些因素。重启动策略有望一并克服这些问题。

含二阶导数变分图像恢复模型的规则项主要包括总广义变差(TGV)(Bredies等，2010)、总拉普拉斯(total Laplacian，TL)(Chan等，2010)、总海森(total Hessian，TH)(Lysaker等，2003)、总平均曲率(total mean curvature，TMC)(Zhu等，2014)和欧拉弹性能(Euler’s elastica，EE)(Yashtini和Kang，2016；Tai等，2011；Kang等，2019)等形式，均为非强凸项，其中，TGV、TL和TH为凸非光滑项，TMC和EE为非凸非光滑项。

本文的目的是以快速ADMM方法为框架，探讨重启动快速算法在这些模型算法设计中应用的可能性。原始ADMM方法的收敛速率为O (1/$k$)，惯性加速方法如快速ADMM理论上可以将收敛速率提高至O (1/$k^2$)。但该类加速方法过分依赖最优惯性参数的设计，一般的变分模型很难估计最优惯性参数，无法找到最优步长，并会产生能量振荡现象，降低收敛速率，无法达到预期效果。重启动算法可以避免振荡现象，从而提高计算效率。

本文针对二阶模型在加速后进行重启动，真正提高算法的收敛速率。重启动快速ADMM方法的时间复杂度的精确分析很困难，故本文选用两种典型的基于拉普拉斯以及基于曲率的二阶模型进行研究，以探讨重启动快速ADMM方法的计算效率问题。本文方法亦可自然拓展到基于类似模型的重启动快速算法。

图像噪声去除是图像恢复的基本问题，图像噪声去除的TV模型(Rudin等，1992)可表达为能量泛函极值问题，具体为

$ \min E(u)=\frac{1}{2}\|u-f\|^{2}+\gamma\|\nabla u\| $

(1)

式中，$\frac{1}{2}\|u-f\|^{2}=\frac{1}{2} \int_{\boldsymbol{\varOmega}}(u-f)^{2} \mathrm{~d} x$为数据项，表示图像恢复前后的接近程度，$\|\nabla u\|=\int_{\boldsymbol{\varOmega}}|\nabla u| \mathrm{d} x$为总变差规则项，作用是保持图像边缘。$f(x): {\mathit{\boldsymbol{\varOmega}}}→{\bf{R}}$为含噪声灰度图像，${\mathit{\boldsymbol{\varOmega}}}$表示图像区域，$u(x): {\mathit{\boldsymbol{\varOmega}}}→{\bf{R}}$为噪声去除后的清晰图像，$γ$为惩罚参数。此外，本文采用内积符号$\langle\boldsymbol{a}, \boldsymbol{b}\rangle=\int_{\boldsymbol{\varOmega}} \boldsymbol{a}(x) \cdot \boldsymbol{b}(x) \mathrm{d} x$。

求解式(1)的ADMM方法(Goldstein等，2014；Buccini等，2020)是通过变量分裂将原优化问题转化为交替方向优化乘子方法，即引入辅助变量${\mathit{\boldsymbol{w}}}=\nabla u$，及Lagrange乘子${\mathit{\boldsymbol{\beta}}}$和惩罚参数$μ$，将其转化为

$ \left\{\begin{aligned} &\left(u^{k+1}, \boldsymbol{w}^{k+1}\right)=\operatorname{argmin} E(u, \boldsymbol{w}) \\ &\boldsymbol{\beta}^{k+1} =\boldsymbol{\beta}^{k}+\mu\left(\boldsymbol{w}^{k+1}-\nabla u^{k+1}\right) \\ &\ \ \ \ k =0, 1, \cdots, K \end{aligned}\right. $

(2)

式中，增广Lagrange函数为

$ \begin{gathered} E(u, \boldsymbol{w})=\frac{1}{2}\|u-f\|^{2}+\gamma\|\boldsymbol{w}\|+\left\langle\boldsymbol{\beta}^{k}, \boldsymbol{w}-\nabla u\right\rangle+ \\ \frac{\mu}{2}\|\boldsymbol{w}-\nabla u\|^{2} \end{gathered} $

在交替优化过程中的两个子优化问题分别为

$ \left\{\begin{array}{l} u^{k+1}=\operatorname{argmin} E\left(u, \boldsymbol{w}^{k}\right) \\ \boldsymbol{w}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}\right) \end{array}\right. $

(3)

采用标准的变分方法，这两个子优化问题可应用一阶方法求解，其收敛率为O (1/$k$)。根据惯性加速思路(Nesterov，1983)，引入中间参数$\alpha^{k}，k=0, 1, …, K$，$\alpha^{0}=1$，且在交替迭代优化过程中修正该参数$\alpha^{k+1}=\frac{1+\sqrt{1+4\left(\alpha^{k}\right)^{2}}}{2}$，以此为基础计算惯性参数$\theta^{k+1}=\frac{\alpha^{k}-1}{\alpha^{k+1}}$，进而更新辅助变量及Lagrange乘子，具体为

$ \left\{\begin{array}{l} \boldsymbol{w}^{k+1} \longleftarrow \boldsymbol{w}^{k+1}+\boldsymbol{\theta}^{k+1}\left(\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right) \\ \boldsymbol{\beta}^{k+1} \longleftarrow \boldsymbol{\beta}^{k+1}+\boldsymbol{\theta}^{k+1}\left(\boldsymbol{\beta}^{k+1}-\boldsymbol{\beta}^{k}\right) \end{array}\right. $

(4)

Goldstein等人(2014)证明，采用该加速方案，其算法的收敛率可提高为O(1/$k^2$)。为了避免涟漪现象，Goldstein等人(2014)设计了重启动方法，并提出判断重启动条件的简单形式的组合残差公式作为简化能量变化的依据。具体为

$ c^{k+1}=\frac{1}{\mu}\left\|\boldsymbol{\beta}^{k+1}-\boldsymbol{\beta}^{k}\right\|^{2}+\mu\left\|\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right\|^{2} $

(5)

该残差公式包括原变量残差$\frac{1}{\mu}\left\|\boldsymbol{\beta}^{k+1}-\boldsymbol{\beta}^{k}\right\|^{2}=\mu\left\|\boldsymbol{w}^{k+1}-\nabla u^{k+1}\right\|^{2}$和对偶变量残差$\mu\left\|\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right\|^{2}$，用于判断迭代是否满足卡罗需—库恩—塔克(Karush-Kuhn-Tucher，KKT)条件(Goldstein等，2014；Buccini等，2020)。为了避免频繁重启，Goldstein等人(2014)和Buccini等人(2020)引入衰减系数$η∈(0, 1)$，当$c^{k+1}<ηc^{k}$时，采用加速方案，否则，通过设置$\alpha^{k+1}=1$“重启动”算法，即

$ \alpha^{k+1}=1, \boldsymbol{w}^{k+1} \longleftarrow \boldsymbol{w}^{k}, \boldsymbol{\beta}^{k+1} \longleftarrow \boldsymbol{\beta}^{k}, c^{k+1} \longleftarrow c^{k} $

(6)

重启动快速ADMM方法不仅可以应用于强凸问题，亦可以应用于非完全凸的问题。当重启动快速ADMM方法应用于非完全凸的问题时，尽管不能像强凸情况那样保证全局收敛速度，但仍然可以确保目标的收敛并且进行加速。在实际的算法设计中，将重启动判断条件严格化为$c^{k+1}=\frac{1}{\mu}\left|\boldsymbol{\beta}^{k+1}-\boldsymbol{\beta}^{k}\right|^{2}+\mu\left|\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right|^{2}$。算法描述如下。

算法1：TV模型的重启动快速ADMM算法

初始化：$u^{0}, \boldsymbol{w}^{0}, \gamma, \boldsymbol{\beta}^{0}, \mu>0$,

$ \alpha^{0}=1, c^{0}>0, \eta \in(0, 1) $

for $k$ = 0，1，2，3，…，do

$ u^{k+1}=\operatorname{argmin} E\left(u, \boldsymbol{w}^{k}\right) ; $

$ \boldsymbol{w}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}\right); $

$ \boldsymbol{\beta}^{k+1} =\boldsymbol{\beta}^{k}+\mu\left(\boldsymbol{w}^{k+1}-\nabla u^{k+1}\right) ; $

$ c^{k+1} =\mu\left|\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right|^{2}+\frac{1}{\mu}\left|\boldsymbol{\beta}^{k+1}-\boldsymbol{\beta}^{k}\right|^{2} ; $

$ \text { if } c^{k+1}<\eta c^{k} \text { then } $

$ \alpha^{k+1}=\frac{1+\sqrt{1+4\left(\alpha^{k}\right)^{2}}}{2} ; $

$ \theta^{k+1}=\frac{\alpha^{k}-1}{\alpha^{k+1}} ; $

$ \boldsymbol{w}^{k+1} \leftarrow \boldsymbol{w}^{k+1}+\theta^{k+1}\left(\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right) ; $

$ \boldsymbol{\beta}^{k+1} \leftarrow \boldsymbol{\beta}^{k+1}+\theta^{k+1}\left(\boldsymbol{\beta}^{k+1}-\boldsymbol{\beta}^{k}\right) ; $

else;

$ \alpha^{k+1}=1 ; $

$ \boldsymbol{w}^{k+1} \longleftarrow \boldsymbol{w}^{k} ; $

$ \boldsymbol{\beta}^{k+1} \longleftarrow \boldsymbol{\beta}^{k} ; $

$ c^{k+1} \longleftarrow \frac{c^{k}}{\eta} ; $

end if;

直到$E(u)$收敛；

end for。

重启动快速ADMM方法的每次迭代属于以下3种类型之一：1)当算法中$c^{k+1}<ηc^{k}$不等式未被满足时，发生“重启动”迭代。2)“未加速”迭代在“重启动”迭代之后立即发生。在这样的迭代中，$\alpha^{k}=1$，因此算法的加速步骤被禁用，使得迭代等同于原始ADMM。3)“加速”迭代是指没有任何“重启”或“未加速”的迭代，在这样的迭代中$\alpha^{k}>1$，算法中$c^{k+1}<ηc^{k}$不等式被满足，调用算法的加速步骤。

这样，算法使用“重启动”方法增强函数值的单调性。这种类似的重启动规则已经用于针对无约束最小化的研究(Kim和Fessler，2018)。

基于二阶导数图像恢复变分TL模型是为克服一阶TV模型的阶梯效应问题提出的(Lysaker等，2003)，其能量泛函极小值问题为

$ \min E(u)=\frac{1}{2}\|u-f\|^{2}+\gamma\|\Delta u\| $

(7)

式中，$\|\Delta u\|$为TL规则项，为非光滑凸泛函。

为了克服TL规则项变分引起的计算困难，引入了两组辅助变量、Lagrange乘子及惩罚参数设计其ADMM算法，以便将原复杂优化问题转化为交替优化的一系列简单子优化问题求解。然后，这些子问题可以通过快速傅里叶变换(fast Fourier transform，FFT)和解析形式的软阈值公式进行求解。

引入辅助变量${\mathit{\boldsymbol{w}}}$和$v$，使$\boldsymbol{w}=\nabla u, v=\nabla \cdot \boldsymbol{w}$，并引入两个Lagrange乘子${\mathit{\boldsymbol{\beta}}}_{1}和β_{2}$，及两个惩罚参数$μ_{1}$和$μ_{2}$，将式(7)转化为ADMM求解方案，即

$ \left\{\begin{array}{l} \left(u^{k+1}, \boldsymbol{w}^{k+1}, v^{k+1}\right)=\operatorname{argmin} E(u, \boldsymbol{w}, v) \\ \boldsymbol{\beta}_{1}^{k+1}=\boldsymbol{\beta}_{1}^{k}+\mu_{1}\left(\boldsymbol{w}^{k+1}-\nabla u^{k+1}\right) \\ \beta_{2}^{k+1}=\beta_{2}^{k}+\mu_{2}\left(v^{k+1}-\nabla \cdot \boldsymbol{w}^{k+1}\right) \\ k=0, 1, \cdots, K \end{array}\right. $

(8)

式中，增广Lagrange函数为

$ \begin{array}{c} E(u, \boldsymbol{w}, v)=\frac{1}{2}\|u-f\|^{2}+\gamma\|v\|+ \\ \left\langle\boldsymbol{\beta}_{1}^{k}, \boldsymbol{w}-\nabla u\right\rangle+\frac{\mu_{1}}{2}\|\boldsymbol{w}-\nabla u\|^{2}+ \\ \left\langle\beta_{2}^{k}, v-\nabla \cdot \boldsymbol{w}\right\rangle+\frac{\mu_{2}}{2}\|v-\nabla \cdot \boldsymbol{w}\|^{2} \end{array} $

式(8)中的3个子优化问题分别为

$ \left\{\begin{array}{l} u^{k+1}=\operatorname{argmin} E\left(u, \boldsymbol{w}^{k}, v^{k}\right) \\ \boldsymbol{w}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}, v^{k}\right) \\ v^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}^{k+1}, v^{k}\right) \end{array}\right. $

(9)

使用标准变分方法求解式(9)第1行，可得关于$u$的Euler-Lagrange方程，具体为

$ \begin{cases}u-f-\mu_{1} \nabla \cdot\left(\nabla u-\boldsymbol{w}^{k}-\frac{\boldsymbol{\beta}_{1}^{k}}{\mu_{1}}\right)=0 & x \in \boldsymbol{\varOmega} \\ \left(\nabla u-\boldsymbol{w}^{k}-\frac{\boldsymbol{\beta}_{1}^{k}}{\mu_{1}}\right) \cdot \boldsymbol{n}=0 & x \in \partial \boldsymbol{\varOmega}\end{cases} $

(10)

令$f^{k}=f-\mu_{1} \nabla \cdot\left(\boldsymbol{w}^{k}+\frac{\boldsymbol{\beta}_{1}^{k}}{\mu_{1}}\right), \boldsymbol{n}$代表边界的单位法矢量。则式(10)可采用快速傅里叶变换求解，即

$ u_{i, j}^{k+1}=R\left(F^{-1}\left(\frac{F\left(f_{i, j}^{k}\right)}{d}\right)\right) $

(11)

式中，$f_{i, j}^{k}=f_{i, j}-\mu_{1} \nabla \cdot\left(\boldsymbol{w}_{i, j}^{k}+\frac{\boldsymbol{\beta}_{1_{i, j}}^{k}}{\mu_{1}}\right), d=1-2 \times \mu_{1}\left(\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}+\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}-2\right)$，$s=0, 1, …, N-1$；$r=0, 1, …, M-1$。文中所采用的图像大小均为$M×N$。

同样，使用标准变分方法求解式(9)第2行，可得关于${\mathit{\boldsymbol{w}}}$的Euler-Lagrange方程，即

$ \begin{cases}\mu_{1}\left(\boldsymbol{w}-\nabla \boldsymbol{u}^{k+1}+\frac{\boldsymbol{\beta}_{1}^{k}}{\mu_{1}}\right)-\mu_{2} \times & \\ \nabla\left(\nabla \cdot \boldsymbol{w}-v^{k}-\frac{\beta_{2}^{k}}{\mu_{2}}\right)=0 & x \in \boldsymbol{\varOmega} \\ \left(\nabla \cdot \boldsymbol{w}-v^{k}-\frac{\beta_{2}^{k}}{\mu_{2}}\right) n=0 & x \in \partial \boldsymbol{\varOmega}\end{cases} $

(12)

该方程组亦可采用FFT求解，即

$ \left\{\begin{array}{l} w_{1_{i, j}}^{k+1}=\mathfrak{R}\left(F^{-1}\left(\frac{a_{22}\left(h_{1_{i, j}}^{k}\right)-a_{12}\left(h_{2_{i, j}}^{k}\right)}{D}\right)\right) \\ w_{2_{i, j}}^{k+1}=\mathfrak{R}\left(F^{-1}\left(\frac{a_{11} F\left(h_{2_{i, j}}^{k}\right)-a_{21} F\left(h_{1_{i, j}}^{k}\right)}{D}\right)\right) \end{array}\right. $

(13)

式中，$h_{1_{i, j}}^{k}=-\mu_{2} \partial_{x}^{+}\left(v_{i, j}^{k}+\frac{\beta_{2_{i, j}}^{k}}{\mu_{2}}\right)+\mu_{1} \partial_{x}^{+}\left(u_{i, j}^{k}\right)-\beta_{1_{1 i, j}^{k}}^{k}$，

$ h_{2_{i, j}}^{k}=-\mu_{2} \partial_{y}^{+}\left(v_{i, j}^{k}+\frac{\beta_{2}^{k}}{\mu_{2}}\right)+\mu_{1} \partial_{y}^{+}\left(u_{i, j}^{k}\right)-\beta_{1_{2 i, j}}^{k}, $

$ \begin{aligned} &D=\operatorname{det}\left(\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right)=\mu_{1}^{2}- \\ &2 \mu_{1} \mu_{2}\left(\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}+\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}-2\right), \end{aligned} $

$ a_{11}=-2 \mu_{2}\left(\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}-1\right)+\mu_{1}, $

$ \begin{aligned} &a_{12}=-\mu_{2}\left(1-\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}+\sqrt{-1} \sin \frac{2 {\rm{ \mathsf{ π} }} r}{M}\right) \times \\ &\left(-1+\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}+\sqrt{-1} \sin \frac{2 {\rm{ \mathsf{ π} }} s}{N}\right), \end{aligned} $

$ \begin{aligned} &a_{21}=-\mu_{2}\left(1-\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}+\sqrt{-1} \sin \frac{2 {\rm{ \mathsf{ π} }} s}{N}\right) \times \\ &\left(-1+\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}+\sqrt{-1} \sin \frac{2 {\rm{ \mathsf{ π} }} r}{M}\right), \end{aligned} $

$ a_{22}=-2 \mu_{2}\left(\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}-1\right)+\mu_{1} 。$

对于式(9)第3行，其解$v$可用解析形式的软阈值公式表示，具体为

$ \begin{gathered} v_{i, j}^{k+1}=\max \left(\left|\nabla \cdot \boldsymbol{w}_{i, j}^{k+1}-\frac{\beta_{2_{i, j}}^{k}}{\mu_{2}}\right|-\frac{\gamma}{\mu_{2}}, 0\right) \times \\ \frac{\nabla \cdot \boldsymbol{w}_{i, j}^{k+1}-\frac{\beta_{2_{i, j}}^{k}}{\mu_{2}}}{\nabla \cdot \boldsymbol{w}_{i, j}^{k+1}-\frac{\beta_{2_{i, j}}^{k}}{\mu_{2}}+\varepsilon} \end{gathered} $

(14)

采用与Goldstein等人(2014)和Buccini等人(2020)相同的思路，可设计TL模型原变量与对偶变量组合残差公式，即

$ \begin{gathered} c^{k+1}=\mu_{1}\left|\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right|^{2}+\mu_{2}\left|v^{k+1}-v^{k}\right|^{2}+\\ \frac{1}{\mu_{1}}\left|\beta_{1}^{k+1}-\beta_{1}^{k}\right|^{2}+\frac{1}{\mu_{2}}\left|\beta_{2}^{k+1}-\beta_{2}^{k}\right|^{2} \end{gathered} $

(15)

由此，得到应用于TL模型的重启动快速ADMM算法，描述如下。

算法2：TL模型的重启动快速ADMM算法

初始化：$u^{0}, \boldsymbol{w}^{0}, v^{0}, \gamma, \boldsymbol{\beta}_{1}^{0}, \beta_{2}^{0}, \mu_{1}>0, \mu_{2}>0$,

$ \alpha^{0}=1, c^{0}>0, \eta \in(0, 1) ; $

for $ k = 0，1，2，3，…，$do

$ u^{k+1}=\operatorname{argmin} E\left(u, \boldsymbol{w}^{k}, v^{k}\right) ; $

$ \boldsymbol{w}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}, v^{k}\right) ; $

$ v^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}^{k+1}, v^{k}\right) ; $

$ \boldsymbol{\beta}_{1}^{k+1}=\boldsymbol{\beta}_{1}^{k}+\mu_{1}\left(\boldsymbol{w}^{k+1}-\nabla u^{k+1}\right) ; $

$ \boldsymbol{\beta}_{2}^{k+1}=\boldsymbol{\beta}_{2}^{k}+\mu_{2}\left(v^{k+1}-\nabla \cdot \boldsymbol{w}^{k+1}\right) ; $

$ \begin{aligned} c^{k+1}=&\mu_{1}\left|\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right|^{2}+\mu_{2}\left|v^{k+1}-v^{k}\right|^{2}+ \\ &\frac{1}{\mu_{1}}\left|\boldsymbol{\beta}_{1}^{k+1}-\boldsymbol{\beta}_{1}^{k}\right|^{2}+\frac{1}{\mu_{2}}\left|\beta_{2}^{k+1}-\beta_{2}^{k}\right|^{2} ; \end{aligned} $

if $c^{k+1}<ηc^{k}$ then;

$ \alpha^{k+1}=\frac{1+\sqrt{1+4\left(\alpha^{k}\right)^{2}}}{2} ; $

$ \theta^{k+1}=\frac{\alpha^{k}-1}{\alpha^{k+1}} ; $

$ \boldsymbol{w}^{k+1} \leftarrow \boldsymbol{w}^{k+1}+\theta^{k+1}\left(\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right) ; $

$ \boldsymbol{\beta}_{1}^{k+1} \leftarrow \boldsymbol{\beta}_{1}^{k+1}+\theta^{k+1}\left(\boldsymbol{\beta}_{1}^{k+1}-\boldsymbol{\beta}_{1}^{k}\right) ; $

$ \boldsymbol{\beta}_{2}^{k+1} \leftarrow \boldsymbol{\beta}_{2}^{k+1}+\theta^{k+1}\left(\boldsymbol{\beta}_{2}^{k+1}-\boldsymbol{\beta}_{2}^{k}\right) ; $

else

$ \alpha^{k+1}=1 ; $

$ \boldsymbol{w}^{k+1} \leftarrow \boldsymbol{w}^{k} ; $

$ \boldsymbol{\beta}_{1}^{k+1} \leftarrow \boldsymbol{\beta}_{1}^{k} ; $

$ \boldsymbol{\beta}_{2}^{k+1} \leftarrow \boldsymbol{\beta}_{2}^{k} ; $

$ c^{k+1} \leftarrow \frac{c^{k}}{\eta} ; $

end if；

直至$E(u)$收敛；

end for。

EE模型结合了TV规则项和曲率项，使用欧拉的弹性项作为规则项，相应的图像噪声去除变分模型为

$ \begin{gathered} \min \limits_{u} E(u)=\frac{1}{2}\|\boldsymbol{u}-\boldsymbol{f}\|^{2}+\\ \left\langle a+b\left(\nabla \cdot\left(\frac{\nabla u}{|\nabla u|}\right)\right)^{2}, |\nabla u|\right\rangle \end{gathered} $

(16)

欧拉弹性能最早由Nitzberg等人(1993)应用于深度图像分割与虚幻轮廓恢复。Masnou和Morel(1998)将其推广到大破损图像修复，Zhu等人(2013)将其推广到图像分割变分模型。EE模型可以有效减少阶梯效应并产生更接近原图的图像，而且可以在去除噪声的同时保留图像的边缘信息。

在上述模型中，欧拉弹性项$\left\langle {a + b{{\left({\nabla \cdot \left({\frac{{\nabla u}}{{|\nabla u|}}} \right)} \right)}^2}, |\nabla u|} \right\rangle $是非凸、非光滑的，这是导致模型(16)计算困难的根源(Kang等，2019)。Tai等人(2011)通过引入一系列辅助变量和松弛后的非线性约束设计了相应的ADMM算法，本文将该方法拓展为快速ADMM方法，并进一步设计重启动快速ADMM方法。

引入辅助变量${\mathit{\boldsymbol{w}}}$，${\mathit{\boldsymbol{p}}}$和$v$，使$\boldsymbol{w}=\nabla u, \boldsymbol{p}=\frac{\boldsymbol{w}}{|\boldsymbol{w}|}$，$v=\nabla \cdot \boldsymbol{p}$，则EE模型式(16)可转化为

$ \begin{gathered} \min E(u)=\frac{1}{2}\|u-f\|^{2}+\left\langle a+b v^{2}, |\boldsymbol{w}|\right\rangle \\ \text { s.t. } \quad \boldsymbol{w}=\nabla u, \boldsymbol{p}=\frac{\boldsymbol{w}}{|\boldsymbol{w}|}, v=\nabla \cdot \boldsymbol{p} \end{gathered} $

(17)

但$\boldsymbol{p}=\frac{\boldsymbol{w}}{|\boldsymbol{w}|}$为非线性非凸约束，直接使用会导致子优化问题求解困难。由于$|\boldsymbol{p}| \leqslant 1$，根据Hölder不等式，约束$\boldsymbol{p}=\frac{\boldsymbol{w}}{|\boldsymbol{w}|}$可松弛为

$ |\boldsymbol{p}| \leqslant 1, |\boldsymbol{w}|-\boldsymbol{p} \cdot \boldsymbol{w} \geqslant 0 $

(18)

为了进一步简化每个子优化问题的目标函数，再引入一个新的辅助向量${\mathit{\boldsymbol{m}}}$代替式(18)中的变量$p$。引入辅助向量${\mathit{\boldsymbol{m}}}$后，模型共有5个约束，即

$ \left\{\begin{array}{l} \boldsymbol{w}=\nabla u \\ |\boldsymbol{w}|-\boldsymbol{m} \cdot \boldsymbol{w} \geqslant 0 \\ v=\nabla \cdot \boldsymbol{p} \\ \boldsymbol{m}=\boldsymbol{p} \\ |\boldsymbol{m}| \leqslant 1 \end{array}\right. $

(19)

为表达方便，引入$\delta(\boldsymbol{m})= \begin{cases}0 & |\boldsymbol{m}| \leqslant 1 \\ \infty & \text { 其他}\end{cases}$表达约束${\mathit{\boldsymbol{m}}}≤1$。

在EE模型中，引入4个辅助变量${\mathit{\boldsymbol{w}}}$，${\mathit{\boldsymbol{p}}}$，$v$和${\mathit{\boldsymbol{m}}}$，4个Lagrange乘子$β_{1}$，$β_{2}$，$β_{3}$和$β_{4}$以及4个惩罚参数$μ_{1}$，$μ_{2}$，$μ_{3}$和$μ_{4}$，采用ADMM将式(17)转化为

$ \left\{\begin{array}{l} \left(u^{k+1}, \boldsymbol{w}^{k+1}, \boldsymbol{p}^{k+1}, v^{k+1}, \boldsymbol{m}^{k+1}\right)= \\ \operatorname{argmin} E(u, \boldsymbol{w}, \boldsymbol{p}, v, \boldsymbol{m}) \\ \boldsymbol{\beta}_{1}^{k+1}=\beta_{1}^{k}+\mu_{1}\left(\left|\boldsymbol{w}^{k+1}\right|-\boldsymbol{m}^{k+1} \cdot \boldsymbol{w}^{k+1}\right) \\ \boldsymbol{\beta}_{2}^{k+1}=\boldsymbol{\beta}_{2}^{k}+\mu_{2}\left(\boldsymbol{w}^{k+1}-\nabla u^{k+1}\right) \\ \boldsymbol{\beta}_{3}^{k+1}=\beta_{3}^{k}+\mu_{3}\left(v^{k+1}-\nabla \cdot \boldsymbol{p}^{k+1}\right) \\ \boldsymbol{\beta}_{4}^{k+1}=\boldsymbol{\beta}_{4}^{k}+\mu_{4}\left(\boldsymbol{m}^{k+1}-\boldsymbol{p}^{k+1}\right) \\ k=0, 1, \cdots, K \end{array}\right. $

(20)

式中，增广Lagrange函数为

$ \begin{gathered} E(u, \boldsymbol{w}, \boldsymbol{p}, v, \boldsymbol{m})=\frac{1}{2}\left\|_{u}-f\right\|^{2}+\left\langle a+b v^{2}, |\boldsymbol{w}|\right\rangle+ \\ \left\langle\beta_{1}^{k}, |\boldsymbol{w}|-\boldsymbol{m} \cdot \boldsymbol{w}\right\rangle+\left\langle\mu_{1}, |\boldsymbol{w}|-\boldsymbol{m} \cdot \boldsymbol{w}\right\rangle+ \\ \left\langle\boldsymbol{\beta}_{2}^{k}, \boldsymbol{w}-\nabla u\right\rangle+\frac{\mu_{2}}{2}\|\boldsymbol{w}-\nabla u\|_{2}^{2}+ \\ \left\langle\beta_{3}^{k}, v-\nabla \cdot \boldsymbol{p}\right\rangle+\frac{\mu_{3}}{2}\|v-\nabla \cdot \boldsymbol{p}\|^{2}+ \\ \left\langle\boldsymbol{\beta}_{4}^{k}, \boldsymbol{m}-\boldsymbol{p}\right\rangle+\frac{\mu_{4}}{2}\|\boldsymbol{m}-\boldsymbol{p}\|_{2}^{2}+\delta(\boldsymbol{m}) \end{gathered} $

应用交替优化技术，式(20)中的5个子优化问题分别为

$ \left\{\begin{array}{l} \boldsymbol{u}^{k+1}=\operatorname{argmin} E\left(u, \boldsymbol{w}^{k}, \boldsymbol{p}^{k}, v^{k}, \boldsymbol{m}^{k}\right) \\ \boldsymbol{w}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}, \boldsymbol{p}^{k}, v^{k}, \boldsymbol{m}^{k}\right) \\ \boldsymbol{p}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}^{k+1}, \boldsymbol{p}, v^{k}, \boldsymbol{m}^{k}\right) \\ v^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}^{k+1}, \boldsymbol{p}^{k+1}, v, \boldsymbol{m}^{k}\right) \\ \boldsymbol{m}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}^{k+1}, \boldsymbol{p}^{k+1}, v^{k+1}, \boldsymbol{m}\right) \end{array}\right. $

(21)

使用标准变分方法求解式(21)第1行，得到关于$u$的Euler-Lagrange方程，即

$ \begin{cases}u-f-\mu_{2} \nabla \cdot\left(\nabla u-\boldsymbol{w}^{k}-\frac{\boldsymbol{\beta}_{2}^{k}}{\mu_{2}}\right)=0 & x \in \boldsymbol{\varOmega} \\ \left(\nabla u-\boldsymbol{w}^{k}-\frac{\boldsymbol{\beta}_{2}^{k}}{\mu_{2}}\right) \cdot \boldsymbol{n}=0 & x \in \partial \boldsymbol{\varOmega}\end{cases} $

(22)

令$u-f^{k}-\mu_{2} \Delta u=0, f^{k}=f-\mu_{2} \nabla \cdot\left(\boldsymbol{w}^{k}+\frac{\boldsymbol{\beta}_{2}^{k}}{\mu_{2}}\right)$，采用快速傅里叶变换求解式(22)，得

$ u_{i, j}^{k+1}=R\left(F^{-1}\left(\frac{F\left(f_{i, j}^{k}\right)}{d}\right)\right) $

(23)

式中，$f_{i, j}^{k}=f-\mu_{2} \nabla \cdot\left(\boldsymbol{w}_{i, j}^{k}+\frac{\boldsymbol{\beta}_{2_{i, j}}^{k}}{\mu_{2}}\right)$，

$d=1-2 \mu_{2}\left(\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}+\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}-2\right), s=0, 1, \cdots$，$N-1; r=0, 1, \cdots, M-1$。文中所采用的图像大小均为$M×N$。

对于式(21)第2行，其解${\mathit{\boldsymbol{w}}}$可用解析形式的广义软阈值公式表示，即

$ \begin{gathered} \boldsymbol{w}_{i, j}^{k+1}=\max \left(\left|\boldsymbol{A}_{i, j}\right|-\frac{a+b\left(v_{i, j}^{k}\right)^{2}+\beta_{1_{i, j}}^{k}+\mu_{1}}{\mu_{2}}, 0\right) \times \\ \frac{\boldsymbol{A}_{i, j}}{\left|\boldsymbol{A}_{i, j}\right|}+\varepsilon \\ \boldsymbol{A}_{i, j}=\nabla u_{i, j}^{k+1}-\frac{\boldsymbol{\beta}_{2_{i, j}}^{k}}{\mu_{2}}+\frac{\beta_{1_{i, j}}^{k}+\mu_{1}}{\mu_{2}} \boldsymbol{m}_{i, j}^{k} \end{gathered} $

(24)

同样，使用标准变分方法求解式(21)第3行，可得关于${\mathit{\boldsymbol{p}}}$的Euler-Lagrange方程，即

$ \left\{\begin{array}{cl} -\mu_{3} \nabla\left(\nabla \cdot \boldsymbol{p}-v^{k}-\frac{\beta_{3}^{k}}{\mu_{3}}\right)+ & \\ \mu_{4}\left(\boldsymbol{m}^{k}-\boldsymbol{p}+\frac{\boldsymbol{\beta}_{4}^{k}}{\mu_{4}}\right)=0 & x \in \boldsymbol{\varOmega} \\ \left(\nabla \cdot \boldsymbol{p}-v^{k}-\frac{\beta_{3}^{k}}{\mu_{3}}\right) \boldsymbol{n}=0 & x \in \partial \boldsymbol{\varOmega} \end{array}\right. $

(25)

该方程组亦可采用FFT求解，即

$ \left\{\begin{array}{l} p_{1_{i, j}}^{k+1}=\mathfrak{R}\left(F^{-1}\left(\frac{a_{22} F\left(h_{1_{i, j}}^{k}\right)-a_{12} F\left(h_{2_{i, j}}^{k}\right)}{D}\right)\right) \\ p_{2_{i, j}}^{k+1}=\mathfrak{R}\left(F^{-1}\left(\frac{a_{11} F\left(h_{2_{i, j}}^{k}\right)-a_{21} F\left(h_{1_{i, j}}^{k}\right)}{D}\right)\right) \end{array}\right. $

(26)

式中，$h_{2_{i, j}}^{k}=-\mu_{3} \partial_{y}^{+}\left(v_{i, j}^{k}+\frac{\beta_{3_{2_{i, j}}}^{k}}{\mu_{3}}\right)-\mu_{4} m_{2_{i, j}}^{k}-\beta_{4_{2_{i, j}}^{k}}^{k}$，

$ h_{1_{i, j}}^{k}=-\mu_{3} \partial_{x}^{+}\left(v_{i, j}^{k}+\frac{\beta_{3_{1_{i, j}}}^{k}}{k}\right)-\mu_{4} m_{1_{i, j}}^{k}-\beta_{4_{1_{i, j}}}^{k}, $

$ \begin{aligned} &D=\operatorname{det}\left(\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right)=\mu_{4}^{2}+2 \mu_{3}\ \mu_{4} \times \\ &\left(\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}+\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}-2\right), \end{aligned} $

$ a_{11}=-2 \mu_{3}\left(\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}-1\right)-\mu_{4}, $

$ \begin{aligned} &a_{12}=-\mu_{3}\left(1-\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}+\sqrt{-1} \sin \frac{2 {\rm{ \mathsf{ π} }} r}{M}\right) \times \\ &\left(-1+\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}+\sqrt{-1} \sin \frac{2 {\rm{ \mathsf{ π} }} s}{N}\right), \end{aligned} $

$ \begin{aligned} &a_{21}=-\mu_{3}\left(1-\cos \frac{2 {\rm{ \mathsf{ π} }} s}{N}+\sqrt{-1} \sin \frac{2 {\rm{ \mathsf{ π} }} s}{N}\right) \times \\ &\left(-1+\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}+\sqrt{-1} \sin \frac{2 {\rm{ \mathsf{ π} }} r}{M}\right), \end{aligned} $

$ a_{22}=-2 \mu_{3}\left(\cos \frac{2 {\rm{ \mathsf{ π} }} r}{M}-1\right)-\mu_{4}。$

使用标准变分方法求解式(21)第4行，可得关于$v$的Euler-Lagrange方程，即

$ 2 b\left|\boldsymbol{w}^{k+1}\right| v+\mu_{3}\left(v-\nabla \cdot \boldsymbol{p}^{k+1}+\frac{\beta_{3}^{k}}{\mu_{3}}\right)=0 $

(27)

相应的解析解为

$ v_{i, j}^{k+1}=\frac{\mu_{3} \nabla \cdot \boldsymbol{p}_{i, j}^{k+1}-\beta_{3_{i, j}}^{k}}{2 b\left|\boldsymbol{w}_{i, j}^{k+1}\right|+\mu_{3}} $

(28)

使用标准变分方法求解式(21)第5行，可得关于${\mathit{\boldsymbol{m}}}$的Euler-Lagrange方程，即

$ -\left(\mu_{1}+\beta_{1}^{k}\right) \boldsymbol{w}^{k+1}+\mu_{4}\left(\boldsymbol{m}-\boldsymbol{p}^{k+1}+\frac{\boldsymbol{\beta}_{4}^{k}}{\mu_{4}}\right)=0 $

(29)

相应的解析解为

$ \tilde{\boldsymbol{m}}_{i, j}^{k+1}=\frac{\mu_{1}+\boldsymbol{\beta}_{1_{i, j}}^{k}}{\mu_{4}} \boldsymbol{w}_{i, j}^{k+1}-\frac{\boldsymbol{\beta}_{4_{i, j}}^{k}}{\mu_{4}}+\boldsymbol{p}_{i, j}^{k+1} $

(30)

为了满足$|\boldsymbol{m}| \leqslant 1$的约束条件，本文在$\tilde{\boldsymbol{m}}_{i, j}^{k+1}$上引入了一个投影公式，具体为

$ \boldsymbol{m}_{i, j}^{k+1}=\frac{\tilde{\boldsymbol{m}}_{i, j}^{k+1}}{\max \left(\left|\tilde{\boldsymbol{m}}_{i, j}^{k+1}\right|, 1\right)} $

(31)

采用与Goldstein等人(2014)和Buccini等人(2020)相同的策略，设计EE模型的原变量和对偶变量组合残差公式，即

$ \begin{gathered} c^{k+1}=\mu_{1}\left|\boldsymbol{p}^{k+1}-\boldsymbol{p}^{k}\right|^{2}+\mu_{2}\left|\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right|^{2}+ \\ \mu_{3}\left|v^{k+1}-v^{k}\right|^{2}+\mu_{4}\left|\boldsymbol{m}^{k+1}-\boldsymbol{m}^{k}\right|^{2}+ \\ \frac{1}{\mu_{1}}\left|\beta_{1}^{k+1}-\beta_{1}^{k}\right|^{2}+\frac{1}{\mu_{2}}\left|\boldsymbol{\beta}_{2}^{k+1}-\boldsymbol{\beta}_{2}^{k}\right|^{2}+ \\ \frac{1}{\mu_{3}}\left|\beta_{3}^{k+1}-\beta_{3}^{k}\right|^{2}+\frac{1}{\mu_{4}}\left|\boldsymbol{\beta}_{4}^{k+1}-\boldsymbol{\beta}_{4}^{k}\right|^{2} \end{gathered} $

(32)

由此，得到应用于EE模型的重启动快速ADMM算法，描述如下。

算法3：EE模型的重启动快速ADMM算法

初始化：$u^{0}, \boldsymbol{w}^{0}, \boldsymbol{p}^{0}, v^{0}, \boldsymbol{m}^{0}, \gamma^{0}, \beta_{1}^{0}, \boldsymbol{\beta}_{2}^{0}, \beta_{3}^{0}, \boldsymbol{\beta}_{4}^{0}$,

$ \begin{aligned} &\left(\mu_{1}, \mu_{2}, \mu_{3}, \mu_{4}\right)>0, \alpha^{0}=1, c^{0}>0, \eta \in\\ (0, 1)& \end{aligned} $

for $k$ = 0，1，2，3，…，do

$ u^{k+1}=\operatorname{argmin} E\left(u, \boldsymbol{w}^{k}, \boldsymbol{p}^{k}, v^{k}, \boldsymbol{m}^{k}\right) ; $

$ \boldsymbol{w}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}, \boldsymbol{p}^{k}, v^{k}, \boldsymbol{m}^{k}\right) ; $

$ \boldsymbol{p}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}^{k+1}, \boldsymbol{p}, v^{k}, \boldsymbol{m}^{k}\right) ; $

$ v^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}^{k+1}, \boldsymbol{p}^{k+1}, v, \boldsymbol{m}^{k}\right) ; $

$ \boldsymbol{m}^{k+1}=\operatorname{argmin} E\left(u^{k+1}, \boldsymbol{w}^{k+1}, \boldsymbol{p}^{k+1}, v^{k+1}, \boldsymbol{m}\right) ; $

$ \beta_{1}^{k+1}=\beta_{1}^{k}+\mu_{1}\left(\left|\boldsymbol{w}^{k+1}\right|-\boldsymbol{m}^{k+1} \cdot \boldsymbol{w}^{k+1}\right) ; $

$ \boldsymbol{\beta}_{2}^{k+1}=\boldsymbol{\beta}_{2}^{k}+\mu_{2}\left(\boldsymbol{w}^{k+1}-\nabla u^{k+1}\right) ; $

$ \beta_{3}^{k+1}=\beta_{3}^{k}+\mu_{3}\left(v^{k+1}-\nabla \cdot \boldsymbol{p}^{k+1}\right) ; $

$ \boldsymbol{\beta}_{4}^{k+1}=\boldsymbol{\beta}_{4}^{k}+\mu_{4}\left(\boldsymbol{m}^{k+1}-\boldsymbol{p}^{k+1}\right) ; $

$ \begin{aligned} c^{k+1}=& \mu_{1}\left|\boldsymbol{p}^{k+1}-\boldsymbol{p}^{k}\right|^{2}+\mu_{2}\left|\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right|^{2}+\\ & \mu_{3}\left|v^{k+1}-v^{k}\right|^{2}+\mu_{4}\left|\boldsymbol{m}^{k+1}-\boldsymbol{m}^{k}\right|^{2}+\\ & \frac{1}{\mu_{1}}\left|\beta_{1}^{k+1}-\beta_{1}^{k}\right|^{2}+\frac{1}{\mu_{2}}\left|\boldsymbol{\beta}_{2}^{k+1}-\boldsymbol{\beta}_{2}^{k}\right|^{2}+\\ & \frac{1}{\mu_{3}}\left|\beta_{3}^{k+1}-\beta_{3}^{k}\right|^{2}+\frac{1}{\mu_{4}}\left|\boldsymbol{\beta}_{4}^{k+1}-\boldsymbol{\beta}_{4}^{k}\right|^{2} ; \end{aligned} $

if $c^{k+1}<\eta c^{k}$ then

$ \alpha^{k+1} =\frac{1+\sqrt{1+4\left(\alpha^{k}\right)^{2}}}{2} ; $

$ \theta^{k+1} =\frac{\alpha^{k}-1}{\alpha^{k+1}} ; $

$ \boldsymbol{w}^{k+1} \leftarrow \boldsymbol{w}^{k+1}+\theta^{k+1}\left(\boldsymbol{w}^{k+1}-\boldsymbol{w}^{k}\right) ; $

$ \beta_{1}^{k+1} \leftarrow \beta_{1}^{k+1}+\theta^{k+1}\left(\beta_{1}^{k+1}-\beta_{1}^{k}\right) ; $

$ \boldsymbol{\beta}_{2}^{k+1} \leftarrow \boldsymbol{\beta}_{2}^{k+1}+\theta^{k+1}\left(\boldsymbol{\beta}_{2}^{k+1}-\boldsymbol{\beta}_{2}^{k}\right) ; $

else

$ \boldsymbol{\alpha}^{k+1}=1; $

$ \boldsymbol{w}^{k+1} \longleftarrow \boldsymbol{w}^{k}; $

$ \beta_{1}^{k+1} \longleftarrow \beta_{1}^{k}; $

$ \boldsymbol{\beta}_{2}^{k+1} \longleftarrow \boldsymbol{\beta}_{2}^{k}; $

$ c^{k+1} \longleftarrow \frac{c^{k}}{\eta}; $

end if；

直到$E(u)$收敛；

end for。

针对TL模型和EE模型在噪声去除和边缘保持等方面的性能已经有了大量研究。本文研究的重点是在相关惩罚参数确定的情况下，在保持原有模型噪声去除性态的基础上，比较原始ADMM、快速ADMM和重启动快速ADMM方法的计算效率。

实验使用了15幅测试图像分别比较了3种方法的计算效率，其结论基本一致。本文选取具有代表性的5组实验进行说明，实验中使用的5幅测试图像来自美国南加州大学信号与图像处理研究所数据库，如图 1所示。用0~255范围内的像素值缩放图像，图 1(b)为方差$D=0.01$的高斯白噪声污染的图像样本，图 1(c)为噪声密度$d=0.01$的椒盐噪声污染的图像样本。因为希望尽可能少地重启动该方法，建议$η$值接近1。在本文给出的所有数值实验中，$η$取值为0.99。

由于TL模型和EE模型的解决方案通常不是唯一的，无法比较均方根差(root mean square error，RMSE)。实验时，使用相对能量误差$\left|E^{k}-E^{k-1}\right| / E^{k}<0.001$作为停止准则，$E^{k}$表示当前第$k$步迭代的原始能量，$E^{k-1}$表示前一步(第$k$-1步)迭代的原始能量。当相对能量误差无法达到停止标准时，算法将在迭代500次后自动停止。

实验使用3.19 GHz CPU，在Windows 10(64位)操作系统下用MATLAB R2016a版本进行。

TL模型如式(7)所示。${\mathit{\boldsymbol{f}}}$表示含噪声的图像时，最小化式(7)的目的是找到与含噪声的图像${\mathit{\boldsymbol{f}}}$相似的去噪后的图像${\mathit{\boldsymbol{u}}}$，同时保证图像光滑、边缘保持，且不会出现边缘的阶梯效应。参数$γ$控制数据项和规则项之间的权衡。模型参数$γ$主要影响图像的质量，为了更清晰地展示惩罚参数$μ_{1}和μ_{2}$与算法性能之间的关系，固定$γ=1$。

快速算法的目标是在保证图像质量不降低的基础上，提高算法的收敛速率从而加快计算效率。以Texture图像(图 1第3行)为例，图 2展示了原始ADMM、快速ADMM和重启动快速ADMM这3种算法应用到TL模型后输出的图像，3种算法的参数取值均为$μ_{1}=5, μ_{2}=0.001, γ=1$，峰值信噪比(peak signal-to-noise ratio，PSNR)分别为26.518、26.542和26.969。

惩罚参数的数值理论上可以无穷大，但由于引入了Lagrange方程，惩罚可以通过Lagrange乘子$β$调节，所以惩罚参数不需要过大。惩罚参数的选择在理论上没有答案，目前都是通过实验调节选取。本实验选取了大量惩罚参数，在不同参数组合的情况下分析3种算法的计算效率。不同的参数对于快速ADMM方法的计算效率影响较大，当$μ_{1}= 5$时，快速ADMM方法均加速无效，对于重启动方法则基本无影响。

表 1为3种算法在TL模型中去除高斯白噪声的性能比较。可以看出: 1)当惩罚参数相同时，对同一模型3种算法的PSNR基本一致，说明快速算法没有破坏原有模型的性态，没有影响原始ADMM算法的图像质量。2)对不同图像选取了大量的惩罚参数。与原始ADMM算法相比，大部分快速ADMM算法的计算效率提高了6%~50%，最高可以提高50%，如实验10—12等。需要注意的是，实验1—3、7—9、13—15、19—21、25—27中，快速ADMM算法加速无效。这是由于快速ADMM算法的最优步长依赖于目标函数的凸性和光滑性，但TL模型是非光滑的，理论上相关的光滑参数和Lipschitz参数很难估计，故快速ADMM算法无法计算最优步长(O’Donoghue和Candès，2015)。3)相同的模型对相同的图像无论取什么参数，重启动快速ADMM算法的迭代次数都是3，运行时间也明显下降，说明重启动快速ADMM算法非常稳健。与原始ADMM算法相比，重启动快速ADMM算法的计算效率提高了100%~433%，最高可以提高433%，如实验4—6等；4)重启动快速ADMM算法将TL模型中的复杂优化问题转化的一系列子问题，通过FFT和解析形式的软阈值公式进行求解，使迭代步数比传统ADMM方法大幅降低。

表 2为3种算法在TL模型中去除椒盐噪声的性能比较。TL模型在消除椒盐噪声中的各项实验数据与消除高斯白噪声的实验数据基本类似。如不同参数对于快速ADMM方法的计算效率影响较大。当$μ_{1}=5$时，快速ADMM方法出现加速无效情况(实验19—20)，但对于重启动方法则基本无影响。从表 2可以看出：1)当惩罚参数相同时，对同一模型3种算法的PSNR基本一致。2)与原始ADMM算法相比，大部分快速ADMM算法的计算效率提高了13%~240%，最优结果为实验30。3)重启动快速ADMM算法的迭代次数都是3，同样说明了重启动快速ADMM算法的稳健性。与原始ADMM算法相比，重启动快速ADMM算法的计算效率提高了100%~466%，最优结果为实验4、5、6、30等。4)结合表 1可以得出，针对不同噪声消除的程序运行效率，快速ADMM与重启动ADMM算法均加速有效。

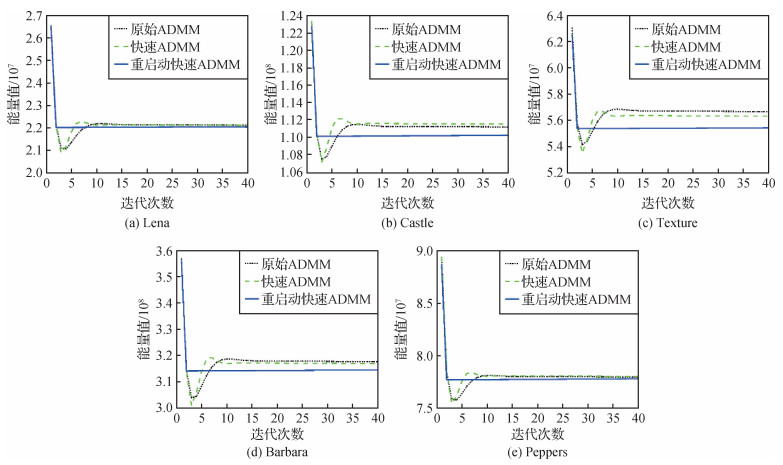
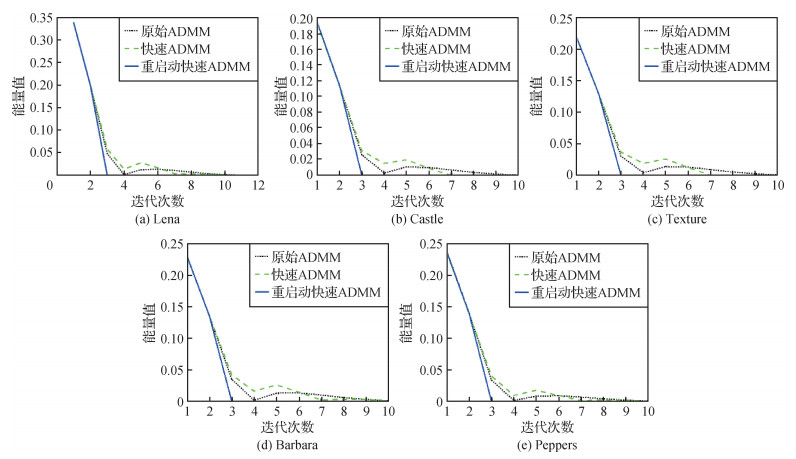
为了可以更清晰地了解在计算过程中3种算法的能量值和相对能量误差的变化趋势，以TL模型消除高斯白噪声为例，对3种算法在TL模型中迭代40次的能量值进行比较，结果如图 3所示。图 4表示使用相对能量误差作为停止准则时，3种算法在TL模型中的收敛曲线。参数取值均为$μ_{1}=5$、$μ_{2}=0.001$、$γ=1$。

从图 3和图 4可以看出，重启动快速ADMM算法的能量值和相对能量误差是单调下降的，且能量值达到稳定状态最快；快速ADMM算法会产生振荡。这是由于TL模型的非光滑性，使光滑参数和Lipschitz参数很难估计，导致振荡的周期很难估计。重启动快速ADMM算法在计算过程中根据组合残差的大小，自适应地调整步长从而消除振荡现象，提高了计算效率。

EE模型如式(16)所示。其中$u, f∈x$分别是未知解和含噪声的数据，$\nabla \cdot \frac{\nabla u}{|\nabla u|}$是水平曲线$u(x, y)=c$的曲率。与基于二阶偏微分方程(partial differential equations，PDE)的方法相比，使用四阶导数可以更快地衰减图像的高频分量，因此式(16)可以减少阶梯效应，并更好地逼近原始图像。实际上，式(16)还能够在减少噪声的同时保留图像边缘。EE模型是最重要的二阶模型之一，为了更清晰地展示惩罚参数$μ_{1}, μ_{2}, μ_{3}, μ_{4}$与算法性能之间的关系，固定$a=0.2, b=2$。

3种算法在EE模型中消除高斯白噪声的性能比较如表 3所示。由于数据过多，表 3只显示Lena图像的数据结果。从表 3可以看出: 1)惩罚参数相同时，对同一模型3种算法的峰值信噪比(PSNR)基本一致，说明快速算法没有影响原始ADMM算法的图像质量。2)惩罚参数不同的情况下，与原始ADMM算法相比，大部分快速ADMM算法的计算效率提高了14%~54%，最优结果为实验13。与TL模型相似，实验2、4中快速ADMM算法在EE模型存在加速无效的情况，EE模型的非凸性和非光滑性加大了计算最优步长的难度。3)相同的模型无论取什么参数，重启动快速ADMM算法的迭代次数都是3，运行时间明显下降，说明重启动快速ADMM算法非常稳健。与原始ADMM算法相比，重启动快速ADMM算法的计算效率提高了100%~900%，最优结果为实验14。4)$μ_{1}$值越小，原始ADMM和快速ADMM算法的计算效率越高，但对于快速重启动ADMM算法基本无影响。

3种算法在EE模型中消除椒盐噪声的性能比较如表 4所示。可以看出: 1)惩罚参数相同时，对同一模型，3种算法的峰值信噪比(PSNR)基本一致。2)与原始ADMM算法相比，大部分快速ADMM算法的计算效率提高了10%~83%，最优结果为实验16。与TL模型相似，快速ADMM算法在EE模型存在加速无效的情况，如实验1、3、10、11。3)结合表 3可以得出，在模型不同、参数不同和噪声不同的情况下，重启动快速ADMM算法的迭代次数都是3，说明重启动快速ADMM算法非常稳健。与原始ADMM算法相比，重启动快速ADMM算法的计算效率提高了66%~800%，最优结果为实验14。

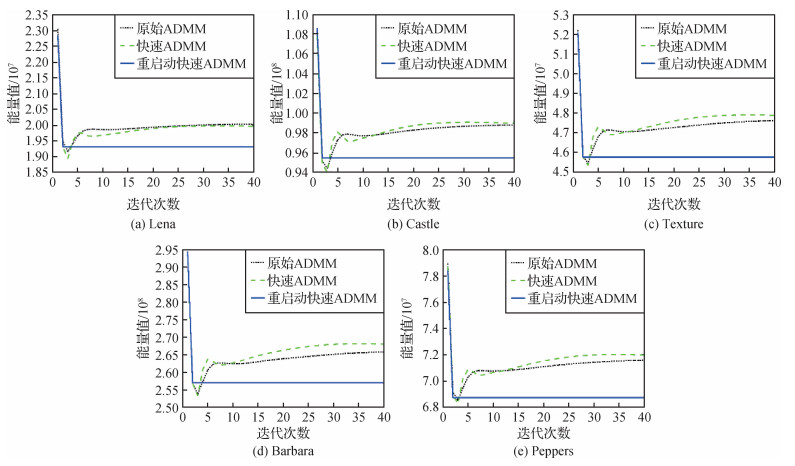
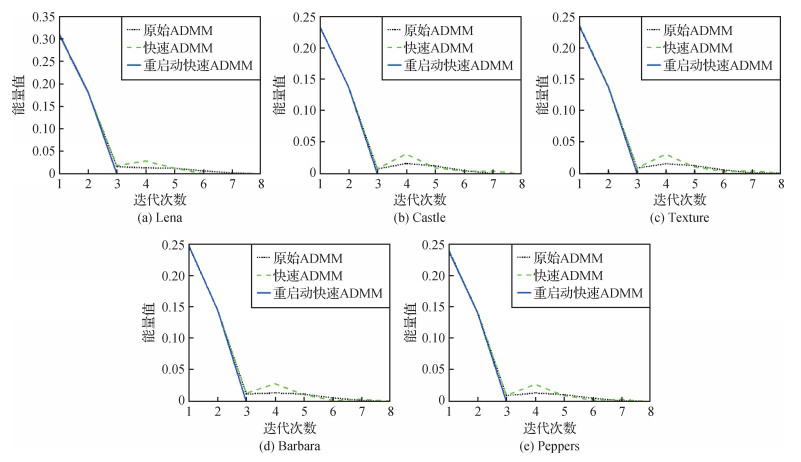
同样，为了可以更清楚地了解在计算过程中3种算法能量值和相对能量误差的变化趋势，以EE模型消除高斯白噪声为例，对3种算法在EE模型中迭代40次的能量值进行比较，结果如图 5所示。图 6表示使用相对能量误差作为停止准则时，3种算法在EE模型中的收敛曲线。参数取值均为$a=0.2$、$b=2$、$μ_{1}=0.06$、$μ_{2}=2$、$μ_{3}=2 000$、$μ_{4}=400$。

从图 5和图 6可以看出: 1)通过函数的能量值曲线，重启动快速ADMM的函数值相较于其他两种算法能够更快地接近稳定。2)快速ADMM算法在图 5的5幅图像中都出现了函数值不单调下降的情况，这种缺陷极大降低了算法效率。这是因为快速ADMM无法计算最优步长，加速步长过大，导致错过了极小值从而出现了函数值不单调下降情况，因此产生振荡。3)重启动快速ADMM算法的能量值和相对能量误差是单调下降的，且能量值达到稳定状态最快。

本文以图像噪声去除为背景，针对含二阶导数规则项的非线性、非光滑的TL模型及非线性、非光滑、非凸的EE模型，以ADMM方法为基础，引入Neserov惯性加速及重启动策略设计了相应的快速算法及重启动快速算法。对不同的变量进行加速，重启动快速算法的计算效率较原始的ADMM方法和快速ADMM方法均有较大提高，为更明显地显示实验效果，本文选取加速效率较为明显的变量进行加速实验。重启动算法的计算效率对所选惩罚参数具有鲁棒性，其计算效率的提高还得益于优化子问题的快速FFT求解及解析形式的软阈值公式的使用。这些有益的探索可为其他形式高阶变分图像处理与分析模型的快速求解提供借鉴。

但是，含高阶导数的非线性、非光滑和非凸变分模型的ADMM方法及其重启动快速算法设计还缺乏足够的理论支撑。目前的理论研究还局限于由两个函数组合的目标函数的优化问题，且确定性的理论成果集中于光滑、强凸及含一个线性约束的优化问题。对于计算机视觉中的含高阶导数的非光滑、非凸变分模型的快速算法研究，本文的工作仅限于尝试性算法设计及数值验证，后续复杂的算法理论分析对算法的推广将具有重要价值。